Guess Who game

Guess Who?

When I was a kid, I owned a game called Guess Who (pictured right).

The idea of the game was simple:

  • Two players face each other, with a board each, containing 24 unique character faces.
  • They mentally pick a character as “their character” for the opponent to guess.
  • They take turns asking simple “yes or no” questions about the characters, to try and isolate their choice, in order to guess correctly and win the game.

The game rules were also simple:

  • Each player gets a single “yes or no” question per turn.
  • They can only Guess Who (to try and win the game) once per game.
  • If a player successfully guesses their opponents character, they win.
  • If their guess is wrong, they lose.

Guess What?

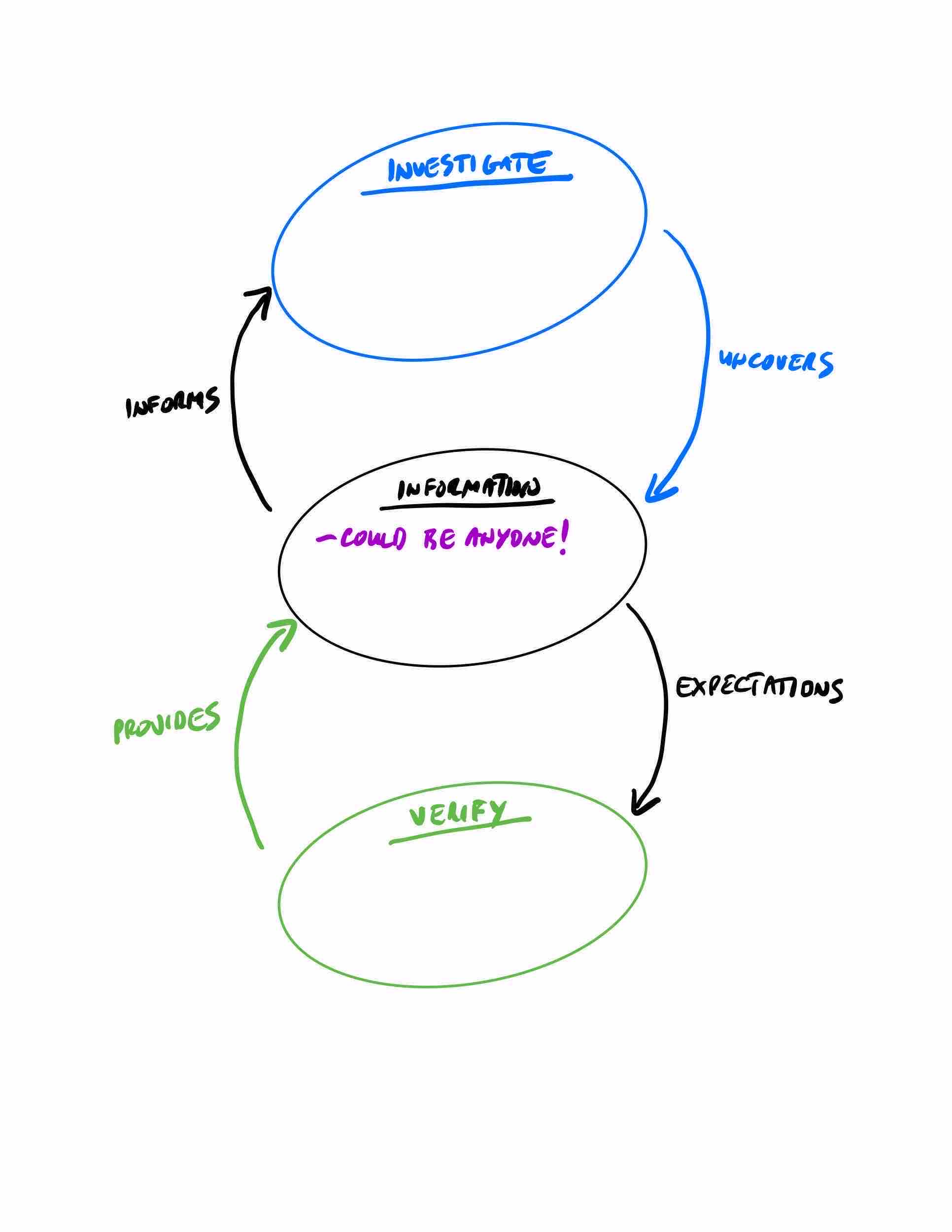
Information Model Stage 1

At the very start of the game, our simplified Information Model has the following bubbles:

  • Investigate = Blank (but we can ask a single question per turn to add to our Information bubble)
  • Information = Could be anyone!
  • Verify = Blank (we can only fill this with a direct guess, and if we’re wrong, we lose)

At this point, we could follow the “Verify” path and try to win the game with a guess:

“I think it’s Susan!”

But this early in the game, a guess would have only a 4% chance of success. It’s therefore in our best interest to ask a single yes/no question, to increase the odds of a correct guess for our next go.

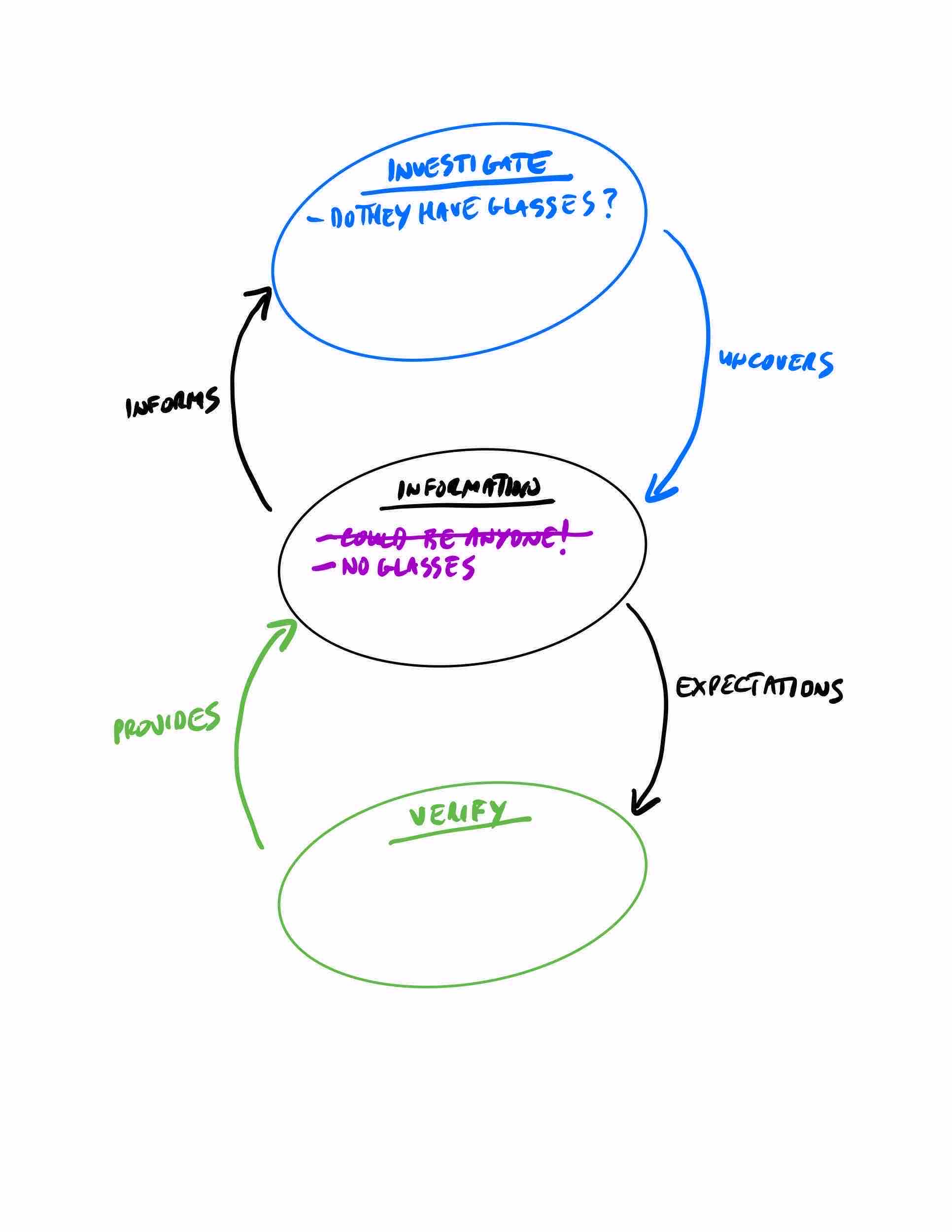
Information Model Stage 2

We decide not to take the risk, and we “Investigate” by asking a question,

“Do they have glasses?”

The answer is “No”, so we push down all 5 faces that have glasses, which leaves 19 still as potential winning guesses.

Our model then looks like this:

  • Investigate = Do they have glasses?
  • Information = NO glasses
  • Verify = Blank (we have not had the confidence to take a guess, yet. Remember, if we’re wrong, we lose instantly!)

On our next turn we have the same choice to make:

  1. Take a guess, at the odds we now have of being correct (5%).
  2. Investigate some more by asking another question.

Are we confident enough in these odds to take the Verify path?

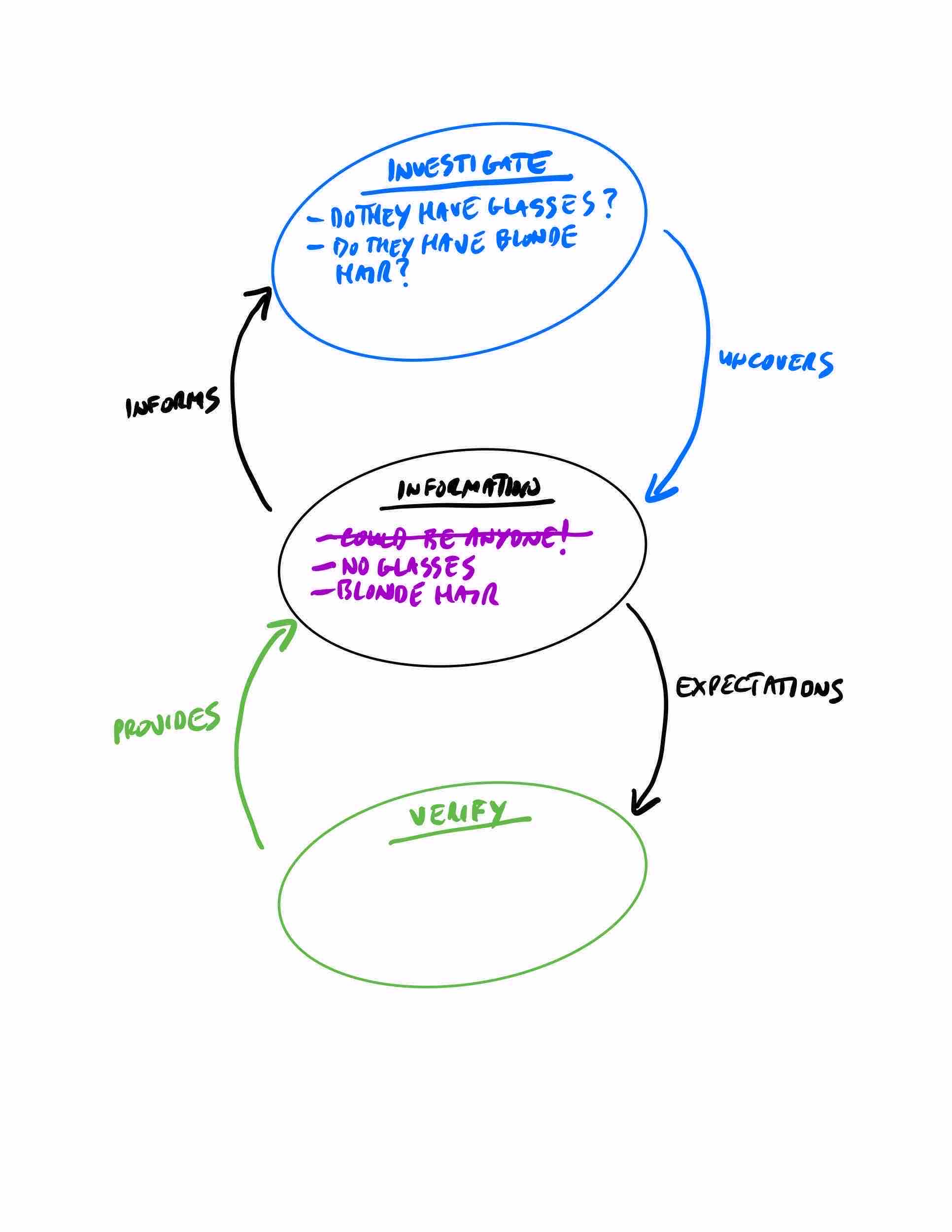
Information Model Stage 3

We decide that we’re not confident enough yet, so we take the Investigate path again and ask another question:

“Do they have blonde hair?”

Aha, they do! So we update our model:

  • Investigate = Do they have glasses? Do they have blonde hair?
  • Information = Do NOT have glasses, DO have blonde hair!
  • Verify = Blank (Again, we did not want to take the risk of guessing)

It’s our turn again and our choice is now:

  1. Go down the Verify path (take a guess), at the odds we now have of being correct (33%)
  2. Investigate some more (ask another question).

Are we confident enough now in these odds to take the Verification path?

And so on…

And so you see that investigation, and analysis, and critical thinking all enable us to make decisions on our next action, until we have enough confidence (acceptance of risk) that we want to follow the next stage of the game - Using our Expectations to Verify that our guess is correct.

Guess Why?

So, why am I reminding you of this random childhood game? Well, the game is an ideal example of the Investigation part of Dan Ashby’s Information Model, and a great way to explain the process of Testing, to non-testers.

As a software development team, we should be creating Information Models on our work. We should be investigating and asking questions, to build our understanding of the task in hand. The more knowledge we have, the more confidence in the solution we might have. We might uncover risks, assumptions, information, things we knew, things we didn’t know, things that might be beneficial, or a hindrance; there are many things we can uncover, which the team can use to create the right solution for the problem.

As information is discovered, we can feed that information back into the “Investigation” to uncover more information, or if information has lead to Expectations, we can feed those into our “Verification” bubble to verify that those expectations are met.

We continue this cycle until we have an acceptance of the risks with the feature we are modelling. Or until we feel that the quality of the feature is good enough.

Guess How?

How would you have played Guess Who if you could guess every turn without forfeit? Would you guess more often? Would you play the same?

How would you play, or how would your Information Model differ, if the character you had to guess was always changing? Or if you had multiple characters to guess?

Or how about if the questions asked could be answered with:

  • Yes
  • No
  • Maybe
  • I refuse to answer